D notation
D notation, or dice notation, is a system to represent different combinations of dice in role-playing games. The system is borrowed from Dungeons & Dragons, as are many aspects of NetHack - the source code implements this as the 'd function' in ref/d. Throughout articles in this wiki, D notation is used to show the probability of an event or the damage of a weapon.
Notation
The notation has the form of ndy, where n and y are variables:
- n is the number of dice rolled
- y is the number of faces on each die
- If n is omitted, its value is 1.
For example, if an article states that a weapon has a damage of 1d24 (roll one die with 24 sides), it can do a damage between 1 and 24. If an article states that a weapon does a damage of 2d24 (roll two dice with 24 sides each), it can do a damage of (1..24) + (1..24). When calculating potential damage from hit dice, hitmu(mhitu.c) sets the attack's base damage to ndy, then mhitm_ad_phys(uhitm.c) adds the weapon damage.
An additional notation that can be encountered is ndy ×2, for the double damage property. For example, Grayswandir has 1d8 ×2 +(1d20) damage. This means that a single die roll of 1d8, plus enchantment, is multiplied by 2; the die is not rolled twice. The 1d20 is added to the result of the multiplication.
Some cases, such as calculating the amount of conditions to be cured by a unicorn horn, will use the result of one or more rolls to determine how many sides will be on a die used for a subsequent roll. For example, a blessed unicorn horn will cure (d(2d4) − 1) ailments. Two four-sided dice will be rolled and their values summed, then a die with the number of sides equal to the prior result will be rolled, and finally one will be subtracted from the result. This produces a range of values weighted toward lower results.
Probabilities
| d(n,x) | |
|---|---|
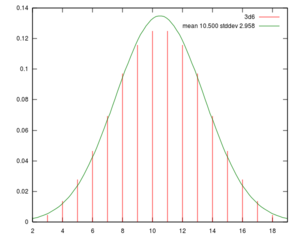 Probability mass function of a roll of 3d6 and probability density function of the normal distribution with the same mean and standard deviation. | |
| Distribution | uniform (n=1) triangular (n=2) approx. normal (n>2) |
| Mean | 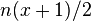
|
| Standard deviation | 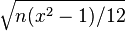
|
Rolling a single die gives any possible roll with equal probability, but multiple dice will tend to give many rolls in the middle of the range and few at the ends. Therefore, rolling 3d6 is not the same as rolling 1d16 and adding 2, even though both give a range from 3 to 18 and a mean (average) of 10.5.
A roll of many dice approximates a normal distribution or "bell curve".
This table gives the probabilities of each possible roll of 3d6:
| Roll | Number of rolls | Probability |
|---|---|---|
| 3 | 1 | 0.00463 |
| 4 | 3 | 0.0139 |
| 5 | 6 | 0.0278 |
| 6 | 10 | 0.0463 |
| 7 | 15 | 0.0694 |
| 8 | 21 | 0.0972 |
| 9 | 25 | 0.116 |
| 10 | 27 | 0.125 |
| 11 | 27 | 0.125 |
| 12 | 25 | 0.116 |
| 13 | 21 | 0.0972 |
| 14 | 15 | 0.0694 |
| 15 | 10 | 0.0463 |
| 16 | 6 | 0.0278 |
| 17 | 3 | 0.0139 |
| 18 | 1 | 0.00463 |
External links
For visualizing or seeing the results of other rolls, see any of the following calculators: