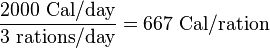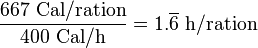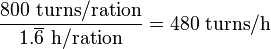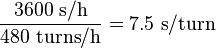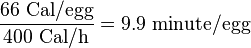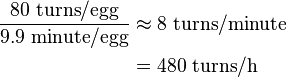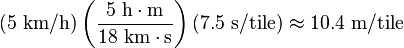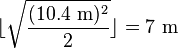NetHack units
Many have tried to convert NetHack units of measurement to a scale that would more or less correlate with real life. This attempt uses metabolism as the transition factor. The result was approximately 7.5 seconds per turn, which seems to be within proper degrees of magnitude. The translated NetHack time will be called Correlated NetHack Time, or CNT.
Contents
Calculation
According to the guidebook, divine intervention was certainly sufficient to influence sleep of the chosen hero ("Strange dreams... haunted you in your sleep"). Therefore, it can be extrapolated that whilst in the dungeon (or Gehennom), magical or divine influence allows the hero to not require regular sleep. This explains why no occurrences of mandatory sleep occur throughout the game.
Assuming, then, that the hero hacks continuously, and that hacking is hard work, the hero's caloric consumption can be calculated. Averaging the energy spent during combat and the energy spent leisurely exploring, the estimated caloric consumption is likely equivalent to that of a brisk walk for a human of 80 kg, or around 400 Cal/hour. (Note that the capital letter is significant here; 1 Calorie (1 Cal) is equal to 1000 calories (1000 cal) or 1 kilocalorie (1 kcal).[1])
Hero consumescontinuously (no sleep).
Computation via food rations
Since food rations are frequently in the hero's inventory from the start, it can be safely assumed that food rations are not magical products, but designed for normal mortal humans to eat three times daily with a daily consumption of 2000 Cal / day.
Because the hero burns through food rations faster than normal humans, each ration can sustain the hero for a much shorter time.
In NetHack, one ration supplies 800 nutritional points, which lasts 800 turns in standard hacking conditions. Therefore,
Alternate computation via eggs
Just how big is a food ration intended to be? The game doesn't really say. One may wish to avoid making assumptions on such an ill-described comestible. If we're after a nutritional reference point in the real world, it makes more sense to use the egg instead.
An average hen egg contains 66 Calories, which would sustain our hero for just a few minutes:
In NetHack, a non-monster egg (which we assume is an ordinary hen egg) supplies 80 nutrition points, which lasts 80 turns:
Which is the same conclusion as we arrived at above.
Extrapolations
With this core value of 7.5 seconds/turn in mind, one can calculate the scale of magnitude of other values in the NetHack world.
An average ascension is 50000 turns, this means that:
4 days and 8 hours of NetHack time seems reasonable for an ascension.
A human walks at approximately 5 km/hour. This means that one NetHack tile is:
This seems reasonable, as a dragon has to fit into one.
A dungeon level's dimension limits are roughly 78×20 varying a little between levels (80×25 minus borders and status lines). This means a dungeon is approximately 810 m by 210 m (roughly, 1/2 mi by 1/8 mi).
Assuming the stairs have an inclination of 45 degrees, the ceiling can be guessed to be about 7 meters high. This result can be found using the Pythagorean theorem a^2 + b^2 = c^2, setting c = 10.4 m and a = b and solving a:
Results
The Hero:
- ... consumes 400 Cal/hour continuously (no sleep).
- ... takes 7.5 seconds to experience one NetHack turn.
- ... ascends in 4 days and 8 hours of Correlated NetHack Time (CNT) on average.
- Maud's record fast ascension took 4 hours, 26 minutes and 52.5 seconds CNT.
- ... eats a full meal every 1 hour 40 minutes CNT.
- ... forgets spells about every 42 hours CNT (no sleep, remember?).
Also:
- A NetHack tile is approximately 10.4 m × 10.4 m × 7 m (34.1 ft. × 34.1 ft. × 23.0 ft.), or 760 m³ (26 740 ft.³).
- Dungeon dimensions are approximately 810 m × 210 m (1/2 mi. × 1/8 mi.).
- The Plane of Water contains about 1.18 billion liters (312 million gallons) of water, weighing 1.18 million metric tons.
- You can throw a zorkmid up to 52 m (170.6 ft) away.
- Moloch's Sanctum can be as deep as 360 m (1181.1 ft) below ground.
For completeness, 8 zorkmids are a dollar.[2]