Exploding die
An exploding die (plural exploding dice) is a mechanic that appears in dNetHack and notdNetHack, and is derived from its use in various forms of tabletop gaming - the mechanic allows one or more dice to be rerolled, typically when that die rolls its highest possible number: that number and the result of the successive roll is added to the total, and rerolled dice also qualify for additional rerolls. This theoretically allows the die roll in question to "explode" repeatedly for incredibly high results if one has exceptional luck.
Other terms for exploding dice include "open-ended rolling" and penetration rolls; a common shorthand for exploding dice in D notation is to use an exclamation point (e.g. 6d6!).
Description
There are two types of exploding dice in dNetHack and notdNetHack: the normal type, as described above, and "Lucky" exploding dice, where the result of the damage die rolls are influenced by your character's in-game Luck - specifically, some low rolls are treated as if they were the maximum roll possible from that die. If the player is being attacked, "Lucky" exploding dice become "Unlucky" exploding dice instead, and the influence of Luck is reversed, i.e. the character's Luck protects them.
Exploding dice are used for the following weapons and attacks, with the exact size of the dice in question varying dependent on the source:
- Attacks using the Scourge of Lolth, which use normal exploding dice
- Attacks using Vorpal Blade or Snickersnee, which use normal exploding dice, but also add +1 total damage per dice roll (both base rolls and bonus rerolls)
- The Fluorite Octet when thrown or slotted into non-artifact lightsabers, beamswords, and double lightsabers, which uses Luck-based exploding dice
- Martial arts attacks while wearing the Grandmaster's Robe, which use normal exploding dice
- Attacks using bare hands while Eurynome is bound, which use normal exploding dice
Strategy
Though in theory a roll for damage with exploding dice has incredibly high potential, in practice exploding dice tend to give much lower returns for bonus damage than one might expect. This does not make it a useless property per se, and the bonus damage can be a welcome aid, but players looking to maximize their average damage-per-round will likely prefer builds that grant high damage floors to those with tantalizingly higher damage ceilings.
Calculating exploding dice and averages
For a given exploding die following the standard rules, the expected value follows geometric distribution, and is expressed as:
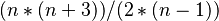
for a given die plus 1. This can be expressed alternatively as
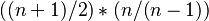
In this second equation, the first set of parenthesis is the is the average damage contributed by each die, and the second set of parenthesis is the average number of times the die explodes.