Exercise
- "Abuse" redirects here. For pet abuse, see Tameness § Abuse.
In NetHack, exercise refers to gradually increasing your attributes over time by repeating certain actions while avoiding performing others.
Contents
Description
Exercising an attribute has a chance of (18 − current attribute value) in 19 of incrementing the attribute's exercise counter, whose maximum value is 50.[1][2] The "current attribute value" also includes modifiers from items - one relevant example is that wearing gauntlets of power has a side-effect of completely preventing strength from being exercised.
You can only exercise four of the six attributes: strength, dexterity, constitution, and wisdom - there is no way to exercise intelligence or charisma, though they can be increased by other means, e.g. a potion of gain ability.
How to exercise
Here are examples of how to efficiently exercise strength, dexterity, constitution, and wisdom:
- Engage in melee combat or push boulders around for strength.
- Hit monsters in melee or with projectiles, or use an unlocking tool to lock or unlock doors or containers for dexterity.
- Eat and avoid becoming hungry or satiated for constitution.
- Cast spells, search for hidden things, or engrave Elbereth with uppercase "E" and lowercase "lbereth" for wisdom.
For more complete lists of exercise methods, see the relevant attribute pages.
Attribute checks
NetHack does exercise checks at certain times: The first check happens on turn 600, and subsequent checks occur at random intervals of 800–999 turns from the last one.[3][4] Upon a check, each counter is examined. If the corresponding attribute is already 18 or greater, nothing is done. Otherwise a random number between 0 and 49 inclusive is chosen. If it is greater than 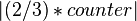 for a non-wisdom attribute or
for a non-wisdom attribute or 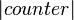 for wisdom, nothing is done. Otherwise, the attribute is changed by adding 1 if the counter was positive and subtracting 1 if it was negative, and the counter is set to zero. Afterwards, no matter what happened, the counter is halved, rounding toward 0.[5]
for wisdom, nothing is done. Otherwise, the attribute is changed by adding 1 if the counter was positive and subtracting 1 if it was negative, and the counter is set to zero. Afterwards, no matter what happened, the counter is halved, rounding toward 0.[5]
Abuse
Abuse is the opposite of exercise - acts of abuse can undo exercise, or even cause your strength, dexterity, constitution, or wisdom to drop.
Each act of abuse has an exactly 50% chance of reducing the attribute's exercise counter by 1.[6] For a comprehensive list of abuse methods, see the relevant attribute pages. If your stats get lowered, use a unicorn horn, potion or spell of restore ability to heal any such loss.
The following information pertains to an upcoming version (NetHack 3.7.0). If this version is now released, please verify that the information below is still accurate, then update the page to incorporate it.
Unicorn horns can no longer restore reduced attributes. Alternatives include potions of restore ability, the restore ability spell, prayer, or finding a way to exercise or increase that attribute again.History
In NetHack 3.4.3, upon loading a saved game, if the first check has happened, the next check was set to happen from 800 (inclusive) to 850 (exclusive) turns afterwards. This meant that saving and reloading the game could have an in-game effect on the player's attributes. As of NetHack 3.6.0, this timer is saved to disk; the effect may persist in some variants based on previous versions.
Variants
UnNetHack
UnNetHack removes the unicorn horn's ability to restore lost stats.
SporkHack
SporkHack also removes the ability of unicorn horns to restore lost stats.
External links
References
- Jump up ↑ src/attrib.c in NetHack 3.6.6, line 426
- Jump up ↑ src/attrib.c in NetHack 3.6.6, line 410
- Jump up ↑ src/allmain.c in NetHack 3.6.6, line 590
- Jump up ↑ src/attrib.c in NetHack 3.6.6, line 608
- Jump up ↑ src/attrib.c in NetHack 3.6.6, line 526
- Jump up ↑ src/attrib.c in NetHack 3.6.6, line 426